[unity]2点間の距離、角度などとりあえず知っておきたいマメ知識

自分もまだまだ勉強中なのですが、とりあえずこれは知っておきたい！　って部分をまとめておきます。（ほとんどクォータニオン Quaternion）

なお、3D 空間ですが XZ 平面で説明します（3 次元でもほぼ同じですが）。

また、基本は自分がいて、敵がいる。という想定で書きますが、自分とカメラなど、「自分がいて、相手がいる」場合は大体同じだと思ってください。

XYZ角度からクォータニオンを求める

var qrot = Quaternion.Eular(0, 30, 0);

クォータニオンは回転に使える便利な情報です（…ってレベルで知っとけばまずはOK！）
transform.rotation も同じクォータニオン。
X:0度、Y:30度、Z:0度のクォータニオンを求めます。

X:0度、Y:30度、Z:0度の移動ポジションを求める

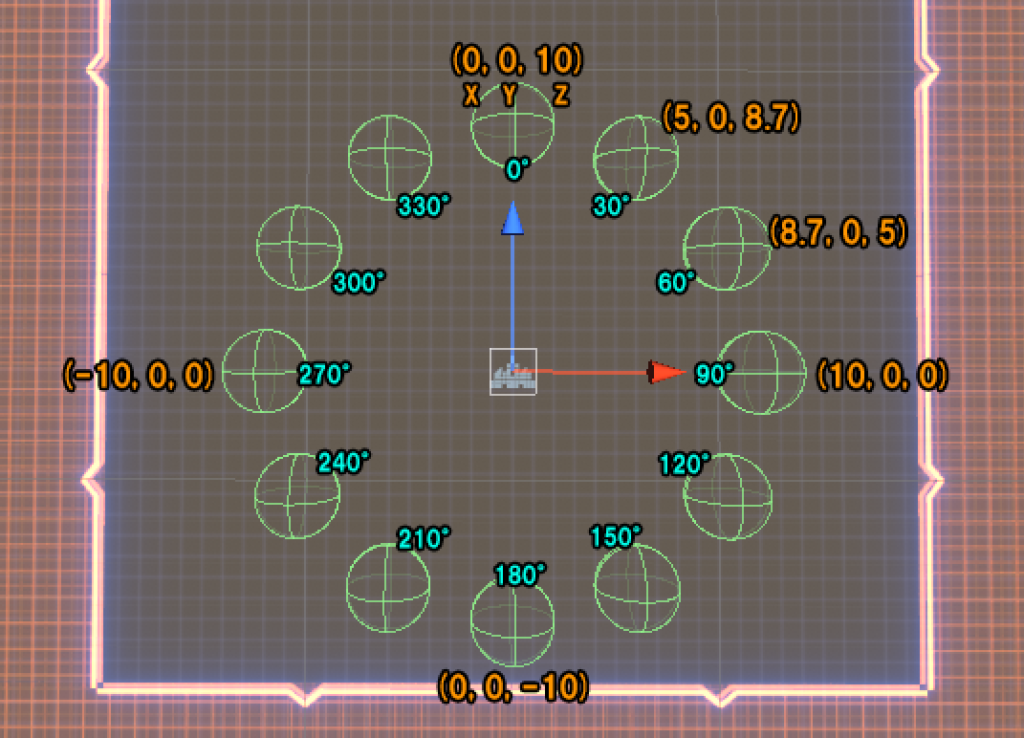
中心を (X: 0, Y: 0, Z: 0) として 0度の時 (X: 0, Y: 0, Z: 10) の位置を Y: 30度回転させたポジションを求めます。
図の右上に示した通り、(X: 5, Y: 0, Z: 8.7) の値が得られます。

var newpos = Quaternion.Euler(0, 30, 0) * new Vector3(0, 0, 10);

注意点として、クォータニオンを先に記述する必要があります。
（Vector3 から先に書いた場合、エラーになります）

// エラーになる
var newpos = new Vector3(0, 0, 10) * Quaternion.Euler(0, 30, 0);

2 点間の距離を求める

float dist_x = enemy.x - player.x;
float dist_z = enemy.z - player.z;

// こちらが正式
float distance = Mathf.Sqrt(dist_x * dist_x + dist_z * dist_z);
if (distance < 100)
{
    // 距離 100 以内だったら
}

// ぶっちゃけこっちで判定した方がコストが安い
float distx2 = dist_x * dist_x + dist_z * dist_z;
if (distx2 < 100 * 100)
{
    // 距離 100 以内だったら
}

3 次元の場合は dist_y * dist_y も足してください。
Mathf.Sqrt を使うと正しい距離が取れますが、「使わなくても乗倍の距離は求められている」ので、distx2 のように使って計算コストを安くすませる事もできます。

2 点間の角度を求める

var qrot = Quaternion.LookRotation(enemy.position - player.position);

これだけでいいらしいぜ…なんて楽なんだ…。

知らなかった頃はこんな感じで書いてました。Mathf.Rad2Deg した上で Quaternion.Eular したり、そもそも 3 次元に（そのままでは）対応できなかったり、いいとこなし。

var diff = (enemy.position - player.position).normalized;
var rot  = Mathf.Atan2(diff.x, diff.z) * Mathf.Rad2Deg;
var qrot = Quaternion.Euler(0, rot, 0);

現在の角度から指定の角度まで滑らかに変化させる

var qrotCurrent = Quaternion.Slerp(enemyTrans.rotation, qrot, 0.01f);

0.01f を大きくすると変化も大きくなります。
敵の向きだけではなく、例えば誘導弾やレーザーなど、幅広く使うことができそうです。

角度を足す

var qrot = Quaternion.Euler(0, 30, 0) * Quaternion.Euler(0, 60, 0);

足し算ではなく掛け算であることに注意してください。上の計算では 90度回転します。